Este es un hermoso y bien documentado trabajo sobre la audaz y revolucionaria figura del maestro Galileo Galilei, en donde su autor: Juan Ignacio Pérez, catedrático de Fisiología en la UPV/EHU y coordinador de la Cátedra de Cultura Científica de la Universidad del País Vasco, nos desgrana vida y circunstancias del Matemático y Astrónomo; una vida que nosotr@s podemos ver y estudiar desde su gráfica Natal.

(La foto del diseño de su configuración astrológica, escrita por el mismo Galileo y la Gráfica Astrológica, las he añadido yo; extraídas de la pág de Astrodienst. Mis notas y comentarios están todos en negrilla).

En la foto de abajo, están los cálculos que el propio Galileo efectuó para levantar la gráfica de su nacimiento.

Galileo fue, sin duda, un personaje excepcional. Aunaba inteligencia, habilidad técnica, ingenio y visión. La inteligencia le permitió entender y relacionar nociones que nadie había manejado o relacionado hasta entonces, así como usar las matemáticas como lenguaje en el que expresar sus resultados. Gracias a su habilidad técnica pudo fabricar excelentes telescopios, los mejores de su época, y gracias a ellos, hacer las observaciones astronómicas que nadie había hecho antes; esa habilidad fue también la que le permitió montar los dispositivos experimentales de sus trabajos sobre la caída de los cuerpos. El ingenio le facilitó el diseño de experimentos muy adecuados al objeto de verificar sus hipótesis y también la elaboración de los argumentos con los que rebate en sus obras las posturas aristotélicas. Y la visión le permitió comprender muchas de las implicaciones filosóficas de sus descubrimientos astronómicos y hallazgos –experimentales o teóricos, para el caso lo mismo da- relativos al movimiento de los cuerpos y la gravedad.

Aunque las referencias bibliográficas –casi de cualquier modalidad- aluden a su papel determinante como introductor del experimento en el estudio de los fenómenos de la naturaleza, sus principales conclusiones las expone mediante razonamientos muy bien elaborados. Tanto el Diálogo como Dos Nuevas Ciencias contienen numerosos ejemplos de argumentación brillante exenta, o casi exenta, de apoyo experimental. Son, de hecho, excelentes ejemplos del método socrático, pues basan en la interpelación y el contraste de pareceres la búsqueda de la verdad.

Y por último, me permito apuntar, como hipótesis, que se trataba de una persona con cierta propensión a la transgresión, a la provocación, al desafío. Esa propensión es quizás la que le dotó de la audacia necesaria para poner sistemáticamente en cuestión las “verdades” aristotélicas, algo que no se había hecho antes de una forma tan sistemática en los campos a los que se dedicó. Pero quizás también fue la causa de los continuos conflictos en que se vio envuelto durante casi toda su vida y la que, en última instancia, motivó su condena y la prohibición del Diálogo.

Galileo Galilei (Pisa, 1564 – Arcetri, 1642) está considerado con todo derecho como uno de los primeros grandes científicos modernos. Forma parte de un conjunto de personajes –Copérnico, Harvey, Kepler, Descartes, Huygens, Boyle y Newton los más relevantes- cuyas ideas y descubrimientos fueron el germen de la ciencia moderna e, incluso, de los mismos fundamentos de la civilización occidental. Pero Galileo, además de por sus descubrimientos e ideas, también es importante porque al ser sus contribuciones al conocimiento tan radicales, no solo tuvo que discutir con sus oponentes acerca de los hechos en sí y su interpretación, sino acerca de las normas adecuadas para establecer esos hechos y para interpretarlos.

En esta anotación y en las que siguen haremos un repaso del personaje, de sus contribuciones al conocimiento, del conflicto que tuvo con la Iglesia y del método –socrático, en buena medida- que utilizó para contrastar sus propuestas.

Además de por sus descubrimientos y por su visión, su carácter, intereses y ambiciones hacían de Galileo un personaje único. Era hijo de una familia acomodada; su padre se ganaba la vida como músico profesional y quiso que su hijo estudiase Medicina para que no se dedicara, como él, a la música. Empezó, de hecho, a estudiar Medicina. Era muy polemista y acostumbraba a cuestionar la sabiduría de la época de tradición aristotélica. Se hizo famoso entre los estudiantes por su afición a discutir, llegando a recibir el apodo de “el pendenciero”. El carácter polemista no le abandonó a lo largo de su vida, lo que fue fuente de problemas y le procuró una buena nómina de enemigos. Además, en parte por razones económicas y en parte, seguramente, por orgullo, durante parte de su carrera puso mucho interés en que se reconocieran sus logros, a poder ser mediante nombramientos que le proporcionasen una situación económica desahogada y un estatus social elevado.

Su carácter polemista y su reticencia –incluso hasta bordear la desobediencia- a aceptar cumplir las órdenes dadas por la Iglesia en relación con la forma en que debía presentar sus puntos de vista sobre las teorías geostatática y geocinética, fue lo que finalmente le llevó a ser condenado a reclusión y a la prohibición de una de sus obras más importantes.

Galileo no se tomó sus estudios muy en serio. Mientras estudiaba Medicina, a principios de 1583, asistió casi de manera casual a una clase de matemáticas de Ostilio Ricci, el matemático de la Corte del Gran Duque de Toscana, y se quedó fascinado con lo que allí escuchó. A partir de aquel momento dejó de lado los estudios de Medicina y se dedicó a estudiar matemáticas. Las matemáticas tuvieron una importancia crucial en su vida y obra. Su enseñanza llegó a ser su modo de vida y fueron la vía por la que se introdujo en la Filosofía Natural. Gran parte de sus logros y de la novedad que supuso su trabajo intelectual radicó en el hecho de que expresase algunos de sus resultados más importantes en lenguaje matemático. Tenía a las matemáticas en tan alta estima que para él eran el lenguaje de la naturaleza: “La Filosofía está escrita en este gran libro, el universo, que se encuentra permanente abierto a nuestra mirada…. Está escrito en el lenguaje de las matemáticas y sus caracteres son triángulos, círculos y otras figuras geométricas sin las cuales es imposible entender ni una sola palabra.” (Il Saggiatore, 1623).

En 1585 se fue de Pisa sin ningún título y volvió a Florencia a ganarse la vida como profesor particular de Matemáticas y Filosofía Natural. En 1589 fue nombrado profesor de Matemáticas en la Universidad de Pisa y, después, de 1592 a 1610, de la Universidad de Padua. Durante esos años se ocupó sobre todo de la naturaleza del movimiento, en general, y de la caída de los cuerpos en particular. En 1604, con 40 años de edad, ya era una autoridad reconocida en Filosofía Natural y en Matemáticas.

Aportaciones

Durante sus años en Padua Galileo realizó los conocidos experimentos con péndulos y con bolas que descendían rodando por planos inclinados. Utilizó esas bolas para demostrar que objetos de distinto peso alcanzan la misma velocidad al estar sometidos a la acción de la fuerza de la gravedad. En su investigación sobre la caída de los cuerpos inició un método que combinaba la observación empírica con la matematización cuantitativa y la teorización conceptual. De esa forma formuló, justificó y hasta cierto punto, sistematizó principios mecánicos tales como los siguientes: una aproximación a la ley de la inercia; la descomposición del movimiento en sus elementos componentes; la ley según la cual al caer un cuerpo la distancia recorrida aumenta en proporción al cuadrado del tiempo transcurrido y que la velocidad adquirida es directamente proporcional al tiempo; y la trayectoria parabólica de los proyectiles.

No publicó ninguno de sus resultados hasta 30 años después, en su Discurso y demostración matemática, en torno a dos nuevas ciencias (1638) [en lo sucesivo Dos nuevas ciencias]. Una de las principales razones para no publicar esos estudios es que a partir de 1609 Galileo se dedicó, sobre todo a realizar estudios astronómicos. Años antes había tenido conocimiento de la teoría de Copérnico, de 1543, según la cuál la Tierra se mueve, y le había interesado la idea de que los datos conocidos relativos a los movimientos de los astros podían ser explicados de forma más coherente y sistemática si se atribuye a la Tierra una rotación axial diaria y una revolución heliocéntrica anual. También pensaba que esa nueva teoría era más consistente con la nueva física que él estaba desarrollando. Pero era consciente de las dificultades de todo orden que entrañaba: era epistemológicamente absurda (contradecía la experiencia sensorial directa), parecía astronómicamente falsa (tenía consecuencias que no se habían podido observar, como la similitud entre los cuerpos terrestres y celestes, las fases de Venus y la paralaje estelar anual); parecía mecánicamente imposible porque los cuerpos, al rotar la tierra, se moverían de forma oblicua al caer libremente y serían expulsados por la fuerza centrífuga. Y además, parecía teológicamente herética, porque contradecía el sentido literal de algunos pasajes de las Escrituras. Hasta 1609 pensaba que los argumentos contrarios pesaban más que los favorables. Sin embargo, en el verano de 1609, cuando era un humilde profesor de matemáticas en la Universidad de Padua, habiendo tenido conocimiento de su existencia, fabricó un telescopio, y empezó a escrutar los cielos con el nuevo instrumento. Esas observaciones fueron las que le llevaron a reevaluar la teoría copernicana. Los descubrimientos astronómicos los publicó en Sidereus nuncius (1610) y durante los siguientes siete años se dedicó a hacer observaciones astronómicas y a participar en intensos debates sobre esas observaciones.

Vio montañas y valles en la Luna, que hay muchísimas más estrellas en el cielo de las que se aprecian a simple vista, que la Vía Láctea y las nebulosas son densos agregados de estrellas, y que Júpiter tiene cuatro lunas orbitando a su alrededor a diferentes distancias y diferentes periodos. Sus observaciones con el telescopio le dieran gran celebridad. Dejó la Universidad de Padua, fue nombrado Matemático y Filósofo del Ducado de Toscana, y se mudo a Florencia ese mismo año. Gracias a la gran notoriedad que alcanzó fue contratado como profesor de Filosofía en la Universidad de Pisa y nombrado Filósofo y Matemático de la Corte por Cosimo de Medici.

Más adelante descubriría las manchas solares y las fases de Venus. Todo ello se lo debía al telescopio y a su extraordinaria capacidad para entender el significado de esas observaciones, algunas de las cuales eran pruebas a favor de la teoría copernicana, pues refutaban las objeciones astronómicas a aquélla y proporcionaban nuevas evidencias observacionales a favor. No obstante, las pruebas no eran concluyentes, pues algunas dificultades persistían: por un lado, había todavía alguna contraevidencia astronómica, como la falta de paralaje estelar anual; por otra parte, la crítica a las objeciones mecánicas y la física de una tierra en movimiento no había sido articulada aún; y por último, no se habían resuelto todavía las objeciones teológicas. Tuvieron que pasar 20 años para que Galileo publicara la obra en la que abordó la discusión de todas estas cuestiones. Esa síntesis fue el Diálogo sobre los dos máximos sistemas del mundo, el ptolemáico y el copernicano (1632) [en adelante, el Diálogo]. Entre tanto se dedicó a polemizar.

El Diálogo se publicó en Florencia y su tesis principal era que los argumentos y las pruebas a favor de la teoría geocinética eran mucho más fuertes que los favorables a la visión geostática, por lo que el movimiento de la tierra es mucho más probable que el geostatismo. Galileo se las arregló para incorporar a la discusión los nuevos descubrimientos telescópicos, sus conclusiones sobre la física de los cuerpos en movimiento, una explicación geocinética de las mareas y varias reflexiones metodológicas.

Para cuando publicó esta obra ya se había ganado una reputación como polemista. Pero en ella fue un poco más allá, pues se basó en las observaciones con el telescopio para apoyar la validez física de la teoría copernicana, aun cuando el permiso para publicar el libro se le había concedido bajo la condición de que presentase el modelo copernicano como un modelo teórico válido para describir los movimientos de los cuerpos del sistema solar, pero sin afirmar nada en relación con su validez física real. Y lo hizo, además, poniendo en boca de Simplicio -el personaje intelectualmente más limitado de los que participan en el diálogo- la posibilidad de que no se trate más que de un buen modelo. El libro fue prohibido y él condenado a retractarse y a reclusión de por vida.

Una consecuencia irónica de la condena fue que volvió a repasar sus notas sobre los experimentos que había hecho más de veinte años antes, los organizó, y cinco años después publicó Dos nuevas ciencias (1638), su principal contribución a la ciencia en el campo de la física, algo que quizás no habría hecho de no haberse producido la condena.

El conflicto con la Iglesia

Para muchos, el juicio a Galileo es un símbolo del empeño de la Iglesia en oponerse al avance de la Ciencia y atrincherarse en una ortodoxia contraria a la razón. Sin embargo, esa interpretación de los hechos que condujeron a la condena no se sostiene a la luz de lo que han aportado los estudios históricos desarrollados en las últimas décadas.

Es cierto que había una controversia relativa a la interpretación de las Escrituras. Los teólogos más conservadores insistieron en el tenor literal de algunos pasajes de la Biblia de los que se desprendía que la Tierra no se movía. El episodio de Josué –cuando ordena al Sol detenerse- es el más citado al respecto. Y Galileo, por su parte, pensaba que las Escrituras no podían considerarse como un libro de Astronomía. Sostenía que habían sido redactadas de manera que fueran coherentes con la experiencia cotidiana de la gente, con independencia de cuál fuera la naturaleza real de los fenómenos o hechos a los que se refería. Y también sugería que había que conceder un papel más importante a la Ciencia a la hora de interpretar los textos sagrados, y esta pretensión chocaba frontalmente con sus oponentes más conservadores.

Pero los problemas no se limitaban a la cuestión de la interpretación de las Escrituras. A la Iglesia no le resultaba fácil aceptar una cosmovisión que chocaba con la que había asumido como verdadera, la aristotélica, según la cual la Tierra se encontraba en el centro del Universo y los cielos la rodeaban en perfecto orden. Si la Tierra no era sino un planeta que gira alrededor del Sol, la imagen de la humanidad como el centro –también físico- de la creación divina se venía abajo. La cosmovisión copernicana abría la puerta a la posible existencia de otros planetas habitados, quizás por seres racionales de cuyas almas y relaciones con Dios nada se sabía. Y esa era una posibilidad que resultaba ciertamente inquietante.

El historiador de la ciencia italiano Pietro Redondi (1988) tras analizar documentos del Vaticano que habían permanecido secretos durante más de tres siglos propuso que el juicio a Galileo no estuvo motivado realmente por las razones aducidas en su momento, sino que obedecía a una causa más profunda. Según Redondi, el juicio fue la consecuencia de que Galileo defendiese una visión mecanicista del Mundo y de otros motivos de más enjundia teológica.

Sea como fuere, en la actualidad está ampliamente aceptado que el juicio a Galileo no fue consecuencia de algo tan simple como el enfrentamiento entre la objetividad científica y el oscurantismo religioso. Por una parte, como hemos visto antes y como ha documentado César Tomé en la serie que se resume aquí, las razones científicas a favor de la cosmovisión copernicana no eran tan contundentes entonces como lo fueron posteriormente. Y no resultaba fácil desprenderse de la visión del Mundo que había sido considerada verdadera desde hacía siglos sin que las pruebas en contra fueran concluyentes. Y por la otra, a Galileo se le había indicado –y él así lo había aceptado- que podía enseñar la teoría copernicana como una hipótesis, esto es, como un instrumento matemático para predecir los movimientos de los planetas, pero que no debía presentarlos como físicamente verdaderos. Y sin embargo, en el Diálogo, no sólo desobedeció esa orden, sino que incluyó pasajes que podían interpretarse como una cierta burla del Papa. Bajo esas circunstancias las autoridades eclesiásticas lo condenaron y le obligaron a retractarse. Fue condenado a arresto domiciliario, y aunque fue amenazado con la torura no llegó a ser torturado. Muchos historiadores sostienen que si Galileo hubiera sido sólo un poco más diplomático, podía haber persuadido a la Iglesia de que suavizase su oposición y las cosas habrían adquirido un rumbo diferente del que tomaron. Al fin y al cabo, dentro de la Iglesia había varias facciones, y aunque unas eran hostiles, otras eran partidarias de Galileo.

Un elemento importante a la hora de valorar todo este asunto es que Galileo era un ferviente creyente y tenía, además, grandes amigos en la jerarquía de la Iglesia. Por lo tanto, no era alguien que estuviera interesado en socavar la autoridad de la jerarquía católica. Pero pensaba, eso sí, que la Naturaleza era una fuente de conocimiento verdadero tan válida como la Biblia. La forma en que él expresaba esta idea es que, al igual que las Escrituras, también el Libro de la Naturaleza había sido escrito por Dios y, por lo tanto, había de ser considerado también como fuente de verdad. Por ello, reivindicaba que los filósofos naturales debían ser considerados expertos a la hora de interpretar los dos textos de autoría divina: la Biblia y la Naturaleza. Así, si el modelo copernicano del Mundo resultaba ser físicamente válido de acuerdo con los mejores intérpretes del Libro de la Naturaleza (los filósofos naturales como él), y dado que dos verdades no podían ser mutuamente contradictorias, Galileo defendía que las referencias bíblicas al carácter estacionario de la Tierra y la movilidad del Sol debían ser tomadas como elementos metafóricos adecuados para ser comprendidos por el pueblo llano. De este modo Galileo pretendía legitimar su papel como experto, sin necesidad de entrar en conflicto con los otros expertos, los teólogos. El Libro de la Naturaleza, que era la fuente de conocimiento de los especialistas en filosofía natural, era, al fin y al cabo, tan fuente de conocimiento divino como las Escrituras. Galileo llegaba incluso a poner por delante al Libro de la Naturaleza, dado que la ambigüedad de los textos bíblicos salía mal parada al compararla con la claridad del otro Libro. Por eso pensaba que el filósofo natural se encontraba en mejor posición que el teólogo a la hora de interpretar la palabra de Dios.

Buenos argumentos

Además de por sus observaciones astronómicas con el telescopio, Galileo ha pasado a la historia como el científico que incorporó los experimentos a su práctica habitual. Este es un aspecto que destacan todos los textos en los que se analiza el personaje. Curiosamente, sin embargo, esa imagen puede resultar un tanto engañosa. Es cierto que era un hábil artesano; sólo así se explica la hazaña que supuso su frenética actividad de construcción de telescopios de alta calidad que mejoraron todos los que se habían hecho anteriormente. Y al ser tan hábil, tenía una gran facilidad para construir dispositivos con los que llevar a cabo ingeniosos experimentos. Sin embargo, es paradójico que su experimento más famoso es casi seguro que no lo llegase a hacer. Me refiero al que, supuestamente, consistió en arrojar dos bolas de diferente peso desde la torre de Pisa.

En todo caso, Galileo era ingenioso y audaz. Y esos rasgos se evidencian con claridad en los experimentos mentales y argumentos que expuso, normalmente en boca del personaje Salviati tanto en el Diálogo como en Dos nuevas ciencias. A continuación y a modo de ejemplo describiré algunos de esos argumentos y experimentos. Me he fijado en algunos de sus experimentos mentales, pero también he incluido el de las bolas rodando por planos inclinados, por la gran importancia que ha tenido en la historia de la ciencia y por haber puesto en juego un dispositivo experimental tan imaginativo. Más adelante también me referiré a algunos errores que cometió, pues no está al alcance de ningún ser humano acertar siempre, y menos aún cuando se piensa con la audacia con la que pensaba nuestro personaje.

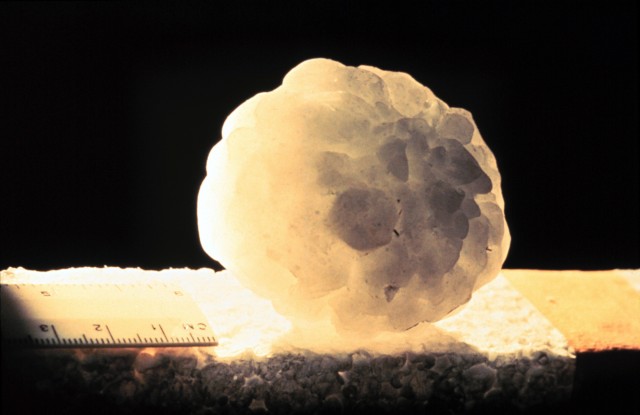
La caída del granizo

En sentido estricto, lo que paso a relatar a continuación no es un experimento mental, pero si un ingenioso argumento. Tal y como de mayor relataba el mismo Galileo, cuando era un joven estudiante de medicina se le ocurrió una idea con la que refutar la teoría aristotélica de que la velocidad de caída de los cuerpos era mayor cuanto mayor era su peso. De ser cierta la anécdota, y al margen de su corrección, revela una notable actitud crítica –y se podría decir que transgresora- para con los conocimientos heredados de Aristóteles y la tradición medieval.

Él se había fijado en que las bolas de granizo, a pesar de tener tamaños diferentes, llegaban al suelo al mismo tiempo, caían a la vez. Esto es, no veía que al empezar a granizar impactaran en el suelo las bolas más grandes en primer lugar, que es lo que tendría que ocurrir en el supuesto de que Aristóteles hubiera tenido razón. La única posibilidad de que la teoría aristotélica fuera correcta era que las bolas de granizo más pesadas se formasen en nubes más altas que aquellas de las que procedían las bolas más ligeras y exactamente a una distancia hacia arriba tal que, cayendo a mayor velocidad, llegaran al suelo junto con las bolas de granizo más ligeras generadas a alturas menores. A Galileo esto le parecía bastante improbable o, al menos, más improbable que la suposición de que todas caían de la misma forma. Y utilizando ese argumento ofrecía a sus compañeros y profesores una explicación mucho más sencilla, según la cual todas las bolas de granizo se producían en el mismo lugar dentro de una nube, por lo que caían todas juntas, independientemente de su peso.

El experimento del barco

Salviati, en el segundo día del Diálogo, expone sus argumentos en contra de la idea aristotélica de que la Tierra no se mueve. Aristóteles había basado esa creencia en el hecho de que al lanzar hacia arriba un objeto y caer verticalmente, no lo vemos caer en un sitio diferente de donde ha sido arrojado. Según Aristóteles si la Tierra se moviera los cuerpos lanzados al cielo caerían a cierta distancia hacia el oeste del punto del que salieron.

Salviati entonces pregunta a Simplicio qué ocurriría en un barco desde cuyo mástil se dejara caer una piedra mientras el barco se mueve. Simplicio responde que la piedra caería lejos de la base del mástil, pues al avanzar el barco dejaría atrás la piedra. Salviati le pregunta si ha comprobado eso en la práctica y tras responderle que no, Simplicio pasa a razonar por qué la piedra habría de caer junto a la base del mástil. A continuación le responde Salviati. Reproduzco a continuación el fragmento del diálogo.

Salviati: “Por lo tanto, un barco que se mueve en un mar en calma es un cuerpo que se desplaza sobre una superficie que no está inclinada ni hacia arriba ni hacia abajo, y así, tiene la tendencia a moverse de forma permanente y uniforme con el impulso que ha adquirido si todos los obstáculos externos son retirados.”

Simplicio: “Parece que así ha de ser”

Salviati: “Ahora, cuando la piedra en la punta del mástil es transportada por el barco, ¿no se mueve ella también a lo largo de la circunferencia de un círculo alrededor de del centro, y en consecuencia con un movimiento indeleblemente inherente a él en tanto los impedimentos externos son retirados? ¿Y no es el movimiento de la misma rapidez que el del barco?

Simplicio: “Hasta aquí, de acuerdo. Pero ¿qué hay del resto?”

Salviati: “Deberías extraer las últimas consecuencias por ti mismo.”

Simplicio: “Por la última conclusión quieres decir que, dado que la piedra se mueve con un movimiento indeleblemente impreso en ella, no lo dejará, sino que seguirá al barco y al final caerá en el mismo punto donde habría caído si el barco hubiera estado quieto; y yo también digo que esto es lo que ocurriría si no hay impedimentos externos que alteren el movimiento de la piedra una vez ha sido dejada caer. Sin embargo, hay dos impedimentos, uno es que el cuerpo en movimiento es incapaz de separar el aire simplemente mediante su ímpetu una vez que pierde el de la potencia de los remos, que era compartido mientras formaba parte del barco cuando todavía estaba en la punta del mástil; el otro es el movimiento de caída recién adquirido, que ha de ser un impedimento a su movimiento horizontal.”

Salviati: “En lo que se refiere al impedimento del aire, no lo niego; y si el cuerpo que cae fuese como una pluma o un mechón de lana, el retraso sería muy grande, pero para una piedra sería muy pequeño. [….].

En lo que se refiere al impedimento del movimiento de caída recién adquirido, en primer lugar está claro que estos dos movimientos (el circular alrededor del centro y el derecho hacia el centro) no son ni contrarios ni incompatibles ni destructivos el uno del otro; porque el cuerpo en movimiento no tiene repugnancia hacia un movimiento tal; tú mismo has asegurado que lo que le repugna es el movimiento que lo aleja del centro (de la Tierra, se entiende); por lo tanto, se deduce necesariamente que al cuerpo en movimiento ni le repugna ni tiene propensión a un movimiento que ni lo acerca ni lo aleja del centro, y por lo tanto no hay razón para que se reduzca la fuerza que lo impulsa. Es más, la causa del movimiento no es única, que podría disminuir en razón de la nueva acción; hay dos causas diferentes, de las que la gravedad sólo conduce al cuerpo hacia el centro, y la fuerza que lo impulsa a moverse alrededor del centro, no hay razón para impedimentos.”

Como se puede ver, Salviati rebate con los suyos los argumentos de Simplicio. Y lo curioso es que aunque al principio le pregunta si ha comprobado en la práctica lo que defiende, él, por su parte, tampoco ha comprobado lo que afirma, pero se vale del debate –no de un experimento- para hacer prevalecer su punto de vista.

En todo caso, lo importante de este experimento mental es que obedece a una noción que es clave en la obra de Galileo, la de la composición de velocidades, algunas de cuyas consecuencias avalaron su corrección. La teoría del movimiento de proyectiles –y más en concreto, sus consecuencias sobre su trayectoria parabólica y sus predicciones sobre el alcance de un disparo de cañón según el ángulo de elevación, corroboradas por la práctica- dependía esa noción.

La caída de dos cuerpos unidos

Antes de entrar a describir los experimentos de las bolas cayendo por planos inclinados, Galileo, en Dos nuevas ciencias, expone –de nuevo en boca de Salviati- un argumento para refutar la idea aristotélica de que cuerpos de diferente masa caen a diferentes velocidades. Lo expone en el día I (Crítica de la ley de caída de Aristóteles):

Simplicio: “No puede haber duda de que un cuerpo que se mueve en un medio tiene una velocidad fijada que está determinada por la naturaleza y que no puede aumentar a no ser que se le proporcione ímpetu o disminuida salvo por la acción de alguna resistencia que la retrase.

Salviati: Entonces, si tomamos dos cuerpos cuyas velocidades naturales son diferentes, está claro que si los juntamos los dos, el más rápido será parcialmente retardado por el más lento, y el más lento, será en alguna medida acelerado por el más rápido. ¿No estás de acuerdo con mi opinión?

Simplicio: estás absolutamente en lo cierto.

Salviati: pero si eso es cierto, y si una piedra se mueve con una velocidad de, digamos, ocho unidades, mientras que una más pequeña se mueve con una velocidad de cuatro, entonces, al unir ambas, el sistema se moverá con una velocidad inferior a ocho unidades. Pero las dos piedras, cuando están unidas hacen una piedra mayor que la que se movía con una velocidad de ocho unidades. Por lo tanto, el cuerpo más pesado se mueve a menos velocidad que el ligero –un efecto que es contrario a tu suposición. Así puedes ver ahora, de tu suposición de que los cuerpos más pesados se mueven más rápidamente que los ligeros yo infiero que los cuerpos más pesados se mueven más lentamente.”

Así pues, Salviati conduce de manera ingeniosa a Simplicio a dar por buenos dos argumentos cuando no puede ser que ambos sean correctos a la vez. Lo que ocurre, claro está, es que ninguno de los dos lo es.

Los experimentos con bolas y planos inclinados

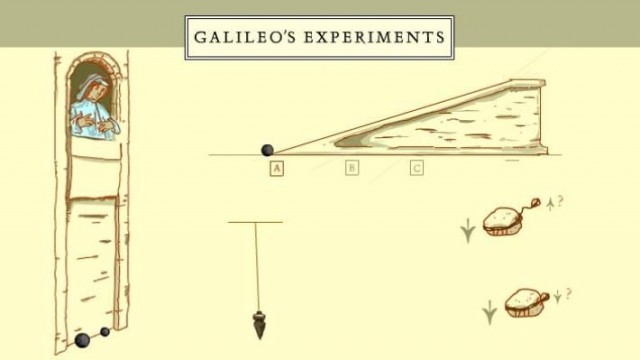
Los experimentos de caída de bolas por planos inclinados han pasado a la historia de la ciencia por un doble motivo. Por un lado, porque mediante ellos Galileo demuestra que los cuerpos caen con una aceleración constante; o, en la forma en que él lo expresó, que cuerpos ideales -sobre los que no actúan fuerzas de rozamiento ni ningún otro factor que interfiera en la caída- recorrerán al caer una distancia que aumenta con el cuadrado del tiempo transcurrido. Esos resultados sirvieron para establecer la mecánica como una ciencia y prepararon el camino para que Newton, unas décadas después, enunciara las leyes de la mecánica y de la gravitación universal. El segundo motivo es que dio carta de naturaleza al experimento y la expresión matemática de los resultados como método de obtención de conocimiento. Experimentos se habían hecho ya antes, también en la Edad Media, contrariamente a lo que mucha gente piensa, pero lo que no se había hecho era expresar los resultados en términos matemáticos, permitiendo de ese modo incorporar un lenguaje objetivo y universal como vehículo de expresión de los hechos científicos.

El problema que había en relación con la caída libre es que la velocidad de caída aumenta muy rápidamente, y si no se cuenta con instrumentos de gran precisión, no es posible medir debidamente el tiempo que tarda el cuerpo que cae en cubrir diferentes distancias. Por esa razón, Galileo buscó un método alternativo y pensó que debía “diluir” el efecto de la gravedad. Para eso se le ocurrió utilizar planos inclinados por los que echaba a rodar bolas y medir el tiempo que tardaba en recorrer ciertas distancias. Los planos con la mínima inclinación son los que permiten mediciones más precisas, ya que son los que más “diluyen” el efecto de la gravedad y propician una velocidad de caída más lenta, siempre, claro está, que se minimice el rozamiento o el efecto de cualquier otro factor que pueda interferir. Pero para poderlo hacer, debía estar seguro de que la caída por planos inclinados tiene propiedades equivalentes a la caída libre, aunque se haya “diluido” el efecto de la gravedad.

Argumentó que la velocidad que adquiere un cuerpo rodando por un plano inclinado no depende de la inclinación del plano, sino de la altura que salva el cuerpo que se deja caer. La idea la extrajo de un experimento con un péndulo al que se añade un clavo en una posición intermedia entre el punto del que pende el hilo y el punto más bajo de la trayectoria del cuerpo que se desplaza (en su caso, una bala de plomo). Al dejarla caer desde el punto de partida, la trayectoria de la bala se altera al llegar el hilo a la posición vertical (y la bala al punto más bajo de la trayectoria), pues en ese momento, el clavo colocado bajo el punto del que pende el hilo se interpone en la trayectoria de éste y obliga a que pivote sobre él, reduciéndose así la longitud del péndulo. Sin embargo, la bala llega a una altura que es la misma que la del punto desde el que partió y, a continuación, reinicia su movimiento pendular retornando al punto de partida, esto es, cuando el péndulo recupera sus condiciones iniciales. La observación crucial aquí es que la velocidad a la que pasa la bola por el punto más bajo de su trayectoria es la misma en las dos direcciones, dado que en ambas alcanza después la misma altura. Esto es, la velocidad con la que llega a ese punto más bajo no varía con la longitud del péndulo, sino con la altura que salva al bajar.

A partir de esa observación, Galileo argumenta que si una bola rueda por un plano inclinado hacia abajo y, a continuación, prosigue su movimiento por otro plano inclinado hacia arriba, la bola alcanzará en su trayectoria la misma altura que la del punto del que partió, de forma similar a como ocurre con el péndulo. Y a semejanza del péndulo truncado, da igual que la pendiente de subida sea más alta o más baja; eso sólo hará variar el cambio en la velocidad (que siempre es máxima en el punto inferior), pero no la altura que salva, que dependerá de la velocidad con que inicia la subida.

Si se ignoran las sucesivas pérdidas de impulso debidas al rozamiento, está claro que en ambas direcciones la bola pasa a la misma velocidad por el punto más bajo de su trayectoria, igual que ocurre en el péndulo, con independencia de cuál sea la pendiente del plano. Así, puede imaginarse un plano cada vez más y más inclinado -con una pendiente cada vez mayor- y la bola siempre llegaría al punto más bajo a la misma velocidad. Pues bien, esa inclinación del plano llevado al extremo consistiría en dejar caer la bola en caída libre: también llegaría la bola al punto más bajo a la misma velocidad.

A partir de esa conclusión ya podía hacer los experimentos en los que medir el tiempo que tardaba una bola en recorrer diferentes distancias. De esa forma estableció la ecuación d = ½ g t2, en la que d es la distancia recorrida por la bola, t es el tiempo que tarda en recorrer esa distancia y g el valor de la aceleración debida a la gravedad, que depende de la inclinación del plano, siendo máxima cuando la caída es libre o, lo que es equivalente, cuando el plano es perpendicular a la superficie de la tierra.

Lo paradójico de estos experimentos es que se han suscitado curiosas dudas sobre ellos. El historiador de la ciencia Alexandre Koyré puso en duda que fueran experimentos reales, pues no creía que los medios con los que contaba Galileo para medir el tiempo fueran tan precisos como para arrojar unos resultados que permitieran obtener la ecuación anterior. Según él es muy posible que Galileo llegase a esa ecuación de forma deductiva y los experimentos, que habrían dado resultados sólo aproximados, tendrían valor meramente ilustrativo o, a lo sumo, habrían servido para verificar que la deducción era básicamente correcta. Peter Dear (1995), por su parte, ha escrito que Galileo no describió ningún experimento ni registró los resultados de forma detallada, sino que se limitó a decir que utilizando un dispositivo determinado, descubrió que los resultados concordaban exactamente con sus supuestos teóricos (dice que repitió las pruebas “cien veces”). Un poco más arriba había escrito que los había hecho “a menudo”, lo que, según Dear, son formas de decir “tantas veces como queráis”. A la hora de valorar estas opiniones más o menos escépticas, conviene recordar también que la deducción de Galileo no es del todo original, sino deudora de la demostración geométrica realizada por Oresme (1323-1382) del llamado Teorema de Merton de la velocidad media(demostrado a su vez en forma algebraica por William de Heytesbury en 1335).

A pesar de las dudas, también ha habido autores que han reproducido los experimentos de la forma en que los describió Galileo y han obtenido resultados precisos y acordes con las expectativas. En todo caso, de lo que no cabe duda es de que Galileo abrió un camino para la ciencia que es el que se ha seguido desde entonces y se ha consolidado como parte esencial de la misma práctica científica. Y este experimento de las bolas resulta, incluso si sólo llegó a ser un experimento mental, desde ese punto de vista, modélico.

Errores

Como he señalado en una anotación anterior, no todas las ideas y argumentos que desarrolló Galileo fueron acertados. Cometió algunos significativos errores, en gran parte por exceso de audacia quizás, ya que en algunos aspectos no contaba con toda la información necesaria para poder formularlos de forma correcta.

Las mareas se deben al movimiento de la Tierra

Una de las razones por las que Galileo era partidario de la teoría geocinética de Copérnico es que pensaba que el movimiento de la tierra –el movimiento combinado de rotación sobre sí misma y de giro alrededor del sol- era lo que mejor explicaba la existencia de las mareas. Tal es así que consideraba que el argumento que relacionaba la subida y bajada de la marea con el movimiento de la Tierra era el más adecuado para desacreditar el geocentrismo ptolemaico. Galileo pensaba que las mareas eran provocadas por las aceleraciones y de deceleraciones de la Tierra que resultaban de la combinación de los movimientos de giro alrededor del sol con los de rotación sobre sí misma. Descarta de partida el posible efecto de la luna (IV día del Diálogo):

“… Hay muchos que atribuyen esto a la Luna, diciendo que ejerce un dominio especial sobre el agua. Últimamente, cierto clérigo (Marcantonio de Dominis, (1566-1624), arzobispo de la ciudad dálmata de Split, que había publicado un libro sobre este tema (Euripus, seu de fluxu et refluxu maris sententia, Roma 1624)) ha publicado un pequeño tratado en el que dice que, al moverse la Luna en el cielo, atrae y eleva hacia sí una masa de agua que la sigue constantemente, de manera que siempre hay marea alta en la parte que se encuentra bajo la Luna; pero puesto que la marea alta retorna cuando se encuentra bajo el horizonte, él sostiene que para explicar ese efecto uno debe decir que la Luna no sólo mantiene esta facultad en ella misma, sino que tiene la facultad de otorgársela al punto opuesto del zodiaco. Como creo que sabes, otros también dicen que la Luna con su moderado calor tiene el poder de rarificar el agua, lo que hace que se eleve al expandirse. También había alguien que….

Sagredo: “Por favor Simplicio, no nos digas nada más, porque no creo que merezca la pena tomarse el tiempo o malgastar palabras para refutarlas; si das tu aprobación a esas o similares nimiedades cometes una injusticia con tu propio juicio, que sabemos que es muy sensato.

Salviati: […..] A ese clérigo le puedes decir que la Luna sobrepasa el Mediterráneo todos los días, pero que las aguas sólo se elevan en su extremo oriental y aquí, para nosotros, en Venecia.”

Salviati argumenta que si el movimiento de las mareas, tal y como sostiene Simplicio, obedece a una causa sobrenatural o milagrosa, es más lógico pensar que la causa milagrosa haría girar a la Tierra sobre su eje, puesto que es más fácil eso que andar elevando y bajando masas de agua dos veces al día; sostiene que hacer esto último implicaría hacer bastantes milagros, mientras que hacer girar la Tierra es sólo uno. Es más, si el milagro consistiese en mover las masas de agua marinas, haría falta otro milagro para evitar que la Tierra se moviera como consecuencia de ello. Por otra parte, discute las otras posibles explicaciones que se han barajado pero concluye que no es posible que se produzca movimiento de mareas sin que se mueva el recipiente de los mares, que es la Tierra. Si un recipiente se mueve de manera que baja o sube uno de sus lados, el agua en su interior se desplaza fluyendo hacia el lado inclinado. Y si el movimiento del recipiente es alterno, el agua irá ahora hacia un lado y luego hacia el otro. Pero esa forma de movimiento no es la que se produciría en los mares de la tierra. Sin embargo hay otra forma que si se produciría cuando el recipiente se mueve hacia adelante a velocidad variable, acelerando y decelerando alternativamente. El agua tendría una cierta capacidad para moverse dentro del recipiente y se movería de manera que al acelerar, el agua tendería a quedar atrás y se elevaría en la parte posterior, y al decelerar pasaría lo contrario. La Tierra se comportaría como un recipiente del agua de los mares. Al experimentar un movimiento de giro alrededor del sol -el de la órbita anual- y otro sobre sí misma -el de la rotación diaria- aunque cada uno de ellos es uniforme, el movimiento resultante (el absoluto) en cada punto de la Tierra no lo es, porque cuando coincide la dirección de ambos movimientos para un punto dado, ese punto se mueve de forma acelerada, pero cuando el de la rotación va en dirección contraria al de la órbita anual, se produce una deceleración. Por lo tanto, el agua de los océanos se moverá hacia arriba y hacia abajo siguiendo el ritmo de aceleración/deceleración. Además, a la subida del agua sigue el descenso pero, una vez iniciado el movimiento, se produce un movimiento de vaivén que hace que las mareas se repitan no cada día, sino cada medio día. La frecuencia de ese movimiento de vaivén dependerá, por otra parte, de la extensión y profundidad del recipiente; eso explicaría el hecho de que las mareas tengan diferentes características en distintas localizaciones geográficas.

En el curso del diálogo, Salviati llega a afirmar que está construyendo una dispositivo que contiene máquinas y recipientes artificiales para poder hacer experimentos combinando diferentes movimientos.

El argumento es ingenioso y está muy bien elaborado, pero es incorrecto. Es precisamente la Luna, por su efecto gravitatorio, la causante de los movimientos mareales, justo el factor que él había despreciado en boca de Sagredo.

El movimiento natural de los cuerpos es circular

Como se ha expuesto más arriba, en los experimentos en que se dejaba caer una bola por un plano inclinado, si a continuación se colocaba un segundo plano inclinado por el que la bola procedente del anterior debía subir, la bola retornaba a la altura de la que había partido, fuese cual fuese la inclinación del plano. Si ese segundo plano inclinado se colocaba de forma que tuviera cada vez menos pendiente, cuanto menor fuera ésta, más lejos tendría que rodar la bola para llegar a su altura inicial. Si el segundo plano fuese horizontal y se pudiera ignorar el rozamiento, la bola rodaría eternamente hacia el horizonte. Y dado que la superficie de la Tierra es esférica, la bola describiría una trayectoria circular. De ahí dedujo Galileo que el movimiento natural de objetos que se desplazan a velocidad constante es circular. Por otro lado, como entendía que la distinción aristotélica entre objetos sublunares y objetos supralunares carecía de sentido, atribuyó ese mismo tipo de movimiento a los objetos celestes. Y al parecer, esa es la razón por la que dio por buena la teoría de Copérnico y no estimó la de Kepler de que los planetas siguen una trayectoria elíptica al girar alrededor del sol.

Este error es cualitativamente diferente del de las mareas y de consecuencias mucho más importantes. Al considerar natural el movimiento circular, Galileo pensó que el movimiento de los planetas no necesitaba ser explicado y quizás por esa razón no llegó a desarrollar una teoría de la gravitación. Fue Newton el que se percató de que en el movimiento de los planetas había un problema que debía ser resuelto; para él sólo era natural el movimiento rectilíneo y uniforme. Y el interés en resolver ese problema fue clave para que acabase formulando una teoría de la gravitación universal.

John Gribbin (2003): Historia de la ciencia 1543-2001 Crítica (Science. A History, 1543-2001, 2002, Allen Lane)

Stephen F. Mason (1985): Historia de las ciencias 2. La revolución científica de los siglos XVI y XVII Alianza Editorial (A History of Sciences, 1962, Hungry Minds Inc)

Javier Ordóñez, Víctor Navarro y José Manuel Sánchez Ron (2003): Historia de la Ciencia Espasa Calpe (el capítulo Edad Moderna es de Víctor Navarro)

John Gribbin (2003): Historia de la ciencia 1543-2001 Crítica (Science. A History, 1543-2001, 2002, Allen Lane)

Stephen F. Mason (1985): Historia de las ciencias 2. La revolución científica de los siglos XVI y XVII Alianza Editorial (A History of Sciences, 1962, Hungry Minds Inc)

Javier Ordóñez, Víctor Navarro y José Manuel Sánchez Ron (2003): Historia de la Ciencia Espasa Calpe (el capítulo Edad Moderna es de Víctor Navarro)

Steven Shapin (1996): The Scientific Revolution The University of Chicago Press

Peter J. Bowler & Iwan R. Morus (2005): Making Modern Science. A Historical SurveyThe University of Chicago Press

Lawrence M. Principe (2012): La revolución científica: Una breve introducción Alianza Editorial (The Scientific Revolution: A very short Introduction, 2011, Oxford University Press)

Steven Shapin (1996): The Scientific Revolution The University of Chicago Press

John Gribbin (2003): Historia de la ciencia 1543-2001 Crítica (Science. A History, 1543-2001, 2002, Allen Lane)

Peter Dear (1995): Discipline and Experience: The Mathematical Way in the Scientific Revolution The University of Chicago Press